Learn Derivative of Sinx Using First Principle
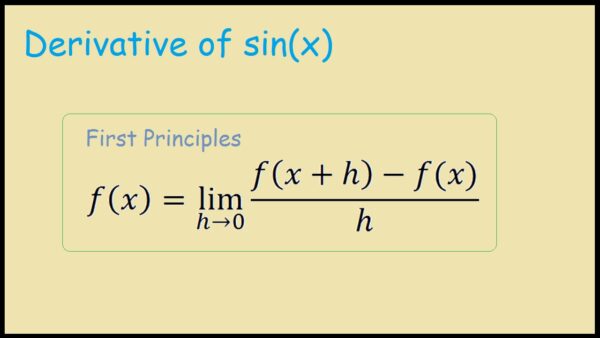
Learn Derivative of Sinx Using First Principle
Differentiation has particular formulas for finding the derivatives of various sorts of functions. One of the differentiation formulas is the derivative of sin x. All of these formulas are derived from the derivative’s limit definition (which is called derivative by the first principle). Using the first premise, we will also prove that the derivative of sin x is -cos x.
The concept of the first principles of derivatives will now be deduced and understood. The concept of derivatives in calculus is based on this premise. Students will be able to apply derivatives to a variety of functions with ease if they have a good understanding of this idea.
Let us learn how to do the derivative of sin x could be done by a few methods. One of them is primarily by using first principles.
What is the Derivative of Root x?
The derivative of root x is d(x)/dx = (1/2) x-1/2 or 1/(2x). The derivative of a function, as we all know, is the process of determining the rate of change of a function with respect to a variable in mathematics. The power rule of differentiation and the first principle of derivatives can be used to find the derivative of root x. We can use the derivative of root x in conjunction with the chain rule technique to estimate the derivative of square root functions.
Derivative of Root x Using First Principle
We shall use the first principle of differentiation to argue that the derivative of root x is equal to (1/2) x-1/2. The derivative of a function f(x) is provided by the formula f'(x) = lim h0 [f(x + h) – f(x)] / h according to the definition of limits, that is, the first principle of derivatives.
Proof of the Derivative of Sin x Using the Chain Rule
According to the chain rule of differentiation, d/dx(f(g(x)) f'(g(x)) g’ (x). So, in order to use the chain rule to calculate the derivative of sin x, we must represent it as a composite function. We can express sin x as, sin x = cos (π/2 – x) using one of the trigonometric formulas. Let us use this to calculate the derivative of y = sin x (or) cos (π/2 – x) (by co-function identity).
By chain rule,
y’ = – sin(π/2 – x) · d/dx (π/2 – x) (as the derivative of cos x is – sin x)
= – sin(π/2 – x) · (-1)
= sin(π/2 – x)
= cos x
By using the chain rule, we were able to get the formula for the derivative of sin x.
Derivative of Root x Using Power Rule
The formula for the power rule of derivatives is d(xn)/dx = nxn-1, where n -1 is power. With x as the base and 1/2 as the power, Root x is an exponential function. Now, if we replace n = 1/2 in the formula d(xn)/dx = nxn-1 with n = 1/2, we get
(1/2) x(1/2) – 1 = d(x1/2)/dx = (1/2) x(1/2) – 1
= x-1/2 x-1/2 x-1/2 x-1/2 x-1/2 x
= 1/(2x)/(2x)/(2x)/(2x)/
As a result, we have established that the derivative of root x equals 1/(2x).
General Differentiation Formula
There are six general differentiation formulas which are as follows:
Power Rule: (ddx)(xn)=nxn−1
Derivation of a constant, a: (ddx)(a)=0
Derivation of a constant increased with function f: (ddx)(a.f)=af′
Sum Rule: (ddx)(f±g)=f′±g′
Product Rule: (ddx)(fg)=fg′+gf′
Quotient Rule: ddx(fg)=gf′–fg′g2
Derivative of 0
There is no derivative for zero. The rate of change is measured by the derivative. Because zero does not change, it cannot have a rate of change. As a result, the derivative of 0 is 0 since the derivative of a constant function may be calculated using the following rule: f(x) = a.