Equation and Solution – x2+(y-3√2x)2=1 Meaning
3 min read
Equation and Solution - x2+(y-3√2x)2=1 Meaning
In the vast and enigmatic realm of mathematics, x2+(y-3√2x)2=1 meaning equations often serve as cryptic riddles awaiting unraveling. Among these mathematical enigmas, the equation x2+(y-3√2x)2=1 meaning stands as a fascinating conundrum.
While its appearance may initially appear complex and daunting, hidden within its seemingly intricate structure are remarkable secrets and practical applications that beckon exploration and comprehension.
Also Read: well health tips in hindi wellhealth
Understanding the Basics of the Equation x2+(y-3√2x)2=1 meaning
Before delving into a thorough examination of the equation’s significance and applications, let’s carefully break down and understand its individual components, establishing a strong basis of comprehension.
The Equation’s Form: A Standard Circle Equation
The equation x2+(y-3√2x)2=1 can be interpreted as a standard form of a circle equation. In this form, it describes a circle with its center positioned precisely at the origin (0,0) and a radius extending to a length of 1.
Breaking Down the Equation into its Constituent Parts
Breaking down the equation into its constituent parts, we discern the following:
- x^2: This component symbolizes the square of the x-coordinate of any point situated on the circle.
- (y – 3√2x)^2: Within this component, we find the square of the difference between the y-coordinate and three times the square root of 2 multiplied by the x-coordinate of a point residing on the circle.
- = 1: This element signifies that the sum of the squares of these two components must precisely equate to the number 1, which is, in essence, the squared value of the circle’s radius.
Graphical Representation: A Visual Odyssey
To facilitate a more intuitive grasp of this equation, let us embark on a visual journey by plotting it onto a Cartesian plane.
Visualizing the Circular Geometry
When plotted, this equation reveals a captivating circular shape. This circle has a radius of 1 unit and is precisely centered at the origin. Essentially, the equation encompasses and delineates all possible points (x2+(y-3√2x)2=1) that perfectly adhere to its mathematical criteria.
The Geometric Center and Radii in Focus
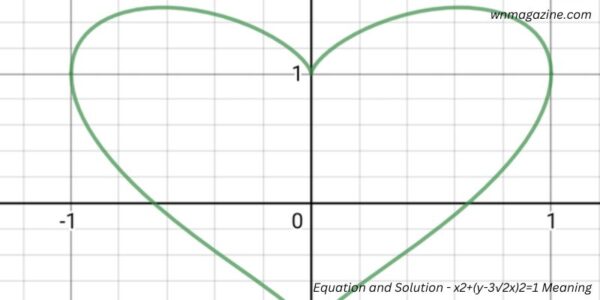
In this circular depiction, the center plays a crucial role, firmly positioned at the coordinate origin (0,0). Serving as the circle’s core, this origin acts as a fixed reference point, while the radius extends outward to a precise distance of 1 unit. Importantly, any point (x, y) located precisely on the circumference of this circular domain inherently conforms to and fulfills the overarching mathematical equation.
Practical Applications: Connecting Mathematics with Real-World Utility
Having explored the mathematical essence and visual representation of this equation, let’s delve into its practical applications across different domains.
Electrical Engineering:
Precision Boundaries In electrical engineering, this equation plays a significant role. Engineers utilize it to define precise boundaries, crucial for demarcating regions of interest. This application is essential in designing circuit boards, x2+(y-3√2x)2=1 where intricate components need strategic positioning and spatial organization.
Also Read: wellhealthorganic vitamin b12
Physics:
Particle Trajectories In physics, the equation x2+(y-3√2x)2=1 takes on an intriguing role. It represents the trajectory of a particle undergoing circular motion. Here, (x, y) collectively represent the dynamic coordinates of the particle at any given moment, revealing the complexities of its circular path.
Geometry:
Crafting Circular Optics The equation’s geometric implications extend to geometry, particularly in crafting circular shapes. These shapes are vital in various optical instruments like circular mirrors and lenses. The equation forms the basis for designing and precisely shaping these optical components.
Conclusion: The Equation’s Significance Unveiled
In closing, the equation x2+(y-3√2x)2=1 though initially shrouded in mathematical mystique, ultimately reveals itself as a fundamental representation of a circle. Its visual depiction, coupled with its diverse applications in electrical engineering, physics, and geometry, collectively illuminate its significance and versatility across multiple disciplines.
About Author
