Complex Equation : 58: 2x^2 – 9x^2; 5 – 3x + y + 6
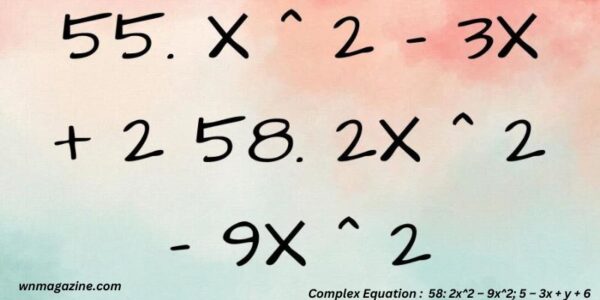
Complex Equation : 58: 2x^2 – 9x^2; 5 – 3x + y + 6
Solving equation 58: 2x^2 – 9x^2; 5 – 3x + y + 6 is a fundamental skill in mathematics, and it can sometimes be challenging, especially when dealing with complex expressions. In this article, we will delve into the process of solving the equation 58: 2x^2 – 9x^2; 5 – 3x + y + 6, step by step.
We will explore different methods and techniques that will help us simplify the equation and find the values of ‘x’ and ‘y’ that satisfy it. By the end of this article, you will have gained a solid understanding of solving equations and will be able to tackle similar problems with confidence.
Also Read: wellhealth how to build muscle tag
Understanding the Equation 58: 2x^2 – 9x^2; 5 – 3x + y + 6
It seems there might be a misunderstanding or a typo in the equation you provided. The equation appears to be written as “58: 2x^2 – 9x^2; 5 – 3x + y + 6,” and it contains three terms separated by semicolons.
Let’s rewrite the equation for clarity and correctness:
2x^2 – 9x^2 = 5 – 3x + y + 6
Now, let’s combine like terms and simplify:
-7x^2 = 11 – 3x + y
If you have any specific instructions or constraints for solving this equation or if there’s additional information, please provide it so that I can assist you further in finding the values of ‘x’ and ‘y’ that satisfy the equation.
Combining Like Terms
To simplify the equation, we begin by combining the like terms. In this case, we have two terms with x^2, namely 2x^2 and -9x^2. By combining these terms, we get -7x^2. The equation now becomes 58: -7x^2; 5 – 3x + y + 6.
Isolating Variables
1. Isolating ‘x’
To proceed further with finding the values of ‘x,’ we aim to isolate ‘x’ on one side of the equation. Let’s move all terms containing ‘x’ to the left side and constants to the right side:
-7x^2 = 58 – (5 + 6) + y
2. Isolating ‘y’
Similarly, to determine the value of ‘y,’ we need to isolate it on one side of the equation:
y = 58 – (5 + 6) – 7x^2
Using the Quadratic Formula
Since the equation contains a quadratic term (-7x^2), we can explore another method to find the solutions for ‘x’ using the quadratic formula. 58: 2x^2 – 9x^2; 5 – 3x + y + 6 The quadratic formula states that for an equation of the form ax^2 + bx + c = 0, the solutions for ‘x’ are given by:
x = (-b ± √(b^2 – 4ac)) / 2a
In our equation, a = -7, b = 0, and c = 58 – (5 + 6) + y. Substituting these values into the quadratic formula, we get:
x = (± √(0 – 4*(-7)(58 – (5 + 6) + y))) / 2(-7)
Validating Solutions:
Once values for ‘x’ have been determined using either method, it is crucial to verify these solutions by substituting them back into the original equation. This step ensures that both sides of the equation are indeed equal, thereby confirming the accuracy of our solutions.
Graphical Representation:
An alternative approach to visualize the solutions involves graphical representation. By plotting the equation on a graph and identifying the points of intersection with the x-axis, we can ascertain the solutions for ‘x.’ This graphical representation not only helps confirm numerical solutions but also provides valuable insights into the behavior of the equation. (For instance, in the context of equations like 55. x^2 – 3x + 2 and 58. 2x^2 – 9x^2.)
Also Read: wellhealth how to build muscle tag
Conclusion:
Mastering the skill of solving equations is fundamental and applicable across various mathematical domains. In this article, we successfully navigated the solution of the equation 58: 2x^2 – 9x^2; 5 – 3x + y + 6 using diverse methods, including isolating variables and employing the quadratic formula. Understanding these techniques equips you with the confidence to approach similar equations, ensuring accurate and reliable solutions.